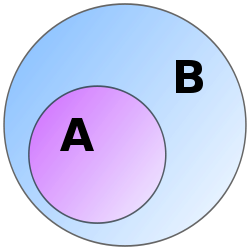
A adalah subset B
Dalam bidang matematik, suatu set adalah subset bagi set jika semua unsur dalam dirangkumi dalam . Hubungan ini dinamakan rangkuman dan ditulis . Pada masa yang sama, adalah superset bagi (ditulis ). Jika bukan subset , hubungan ini ditulis .
Set adalah subset wajar bagi set jika adalah subset tetapi tidak sama dengan . Hubungan ini ditulis . Pada masa yang sama, adalah superset wajar bagi (ditulis ).
Contoh-contoh
- {1, 2} adalah subset wajar {1, 2, 3}.
- Setiap set adalah subset dirinya sendiri, tetapi bukan subset wajar.
- Set kosong, ditulis ∅, adalah subset bagi semua set. Set kosong sentiasa merupakan subset wajar bagi semua set, kecuali dirinya sendiri.
- Set { : adalah nombor perdana yang lebih besar daripada 2000} adalah subset wajar { : adalah nombor ganjil yang lebih besar daripada 1000}.
- Set bagi semua nombor asli, adalah subset wajar bagi set semua nombor nisbah, , dan set bagi semua titik pada suatu tembereng garis adalah subset wajar bagi set semua titik pada satu garis. Ini adalah contoh-contoh aneh (melawan gerak hati) di mana kedua-dua set adalah tak terhingga dan mengandungi unsur yang sama banyak. Lihat kekardinalan set tak terhingga.
Set kuasa
Set bagi semua subset dinamakan set kuasa bagi dan ditulis . Sebagai contoh, set kuasa bagi {1, 2, 3} ialah {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.



















