Liukan - Wikipedia Bahasa Melayu, ensiklopedia bebas

Liukan merupakan perubahan orientasi paksi perputaran sesebuah jasad yang berputar. Dalam rangka rujukan yang bersesuaian ia boleh ditentukan sebagai perubahan dalam sudut Euler yang pertama, sedangkan sudut Euler yang ketiga menentukan putarannya. Dalam erti kata lain, paksi perputaran jasad yang meliuk itu mengitari satu lagi paksi. Pergerakan yang mana sudut Euler kedua berubah itu dipanggil egahan atau nutasi. Dalam bidang fizik terdapat dua jenis liukan, iaitu yang bebas tork dan yang teraruh tork.

Dalam bidang astronomi, "liukan" bermaksud sebarang perubahan perlahan pada parameter perputaran atau orbit sesebuah jasad samawi, terutamanya liukan ekuinoks Bumi.

Bebas tork

Dalam liukan bebas tork, momentum sudut kekal tetap tetapi vektor halaju sudut berubah. Ini dimungkinkan oleh momen inersia yang berubah dengan masa, ataupun yang lebih persisnya, matriks inersia yang berubah dengan masa Matriks inersia terdiri daripada momen-momen inersia yang dihitung berhubung dengan paksi-paksi koordinat (cth. x, y, z), ataupun set-set asas. Jika objek itu tidak simetri di keliling paksi perputaran prinsipalnya, maka momen inersia berhubung dengan setiap asas berubah dengan masa sambil memelihara momentum sudut. Hasilnya adalah halaju-halaju komponen sudut di keliling setiap paksi akan berubah secara songsang kepada momen inersia setiap paksi. Elipsoid Poinsot adalah analog geometri bagi fungsi-fungsi yang menentukan pergerakan bebas tork sesebuah jasad berputar.

Kadar liukan bebas tork sesebuah objek dengan paksi simetri (seperti cakera) yang berputar di keliling paksi yang tidak terjajar dengan paksi simetri itu boleh dihitung seperti berikut:

{\boldsymbol {\omega }}_{p}={\frac {{\boldsymbol {I}}_{s}{\boldsymbol {\omega }}_{s}}{{\boldsymbol {I}}_{p}\cos({\boldsymbol {\alpha }})}}

^[1]

yang mana $\scriptstyle {\boldsymbol {\omega }}_{p}$ = kadar liukan, $\scriptstyle {\boldsymbol {\omega }}_{s}$ = kadar putaran di keliling paksi simetri, $\scriptstyle {\boldsymbol {I}}_{s}$ = momen inersia di keliling paksi simetri, $\scriptstyle {\boldsymbol {I}}_{p}$ = momen inersia di keliling mana-mana daripada dua paksi prinsipal serenjang sama yang lain, dan ${\boldsymbol {\alpha }}$ = sudut di antara momen arah inersia dan paksi simetri.^[2]

Untuk objek yang tidak pejal sepenuhnya, vorteks-vorteksnya akan mudah menlemahkan liukan bebas tork sementara paksi perputarannya menjajarkan dirinya kepada salah satu paksi inersia dalam jasad objek.

Untuk objek pejal biasa tanpa sebarang paksi simetri, evolusi orientasi objek itu yang (sebagai contoh) diwakili oleh matriks putaran $\scriptstyle {\boldsymbol {R}}$ yang menukarkan koordinat dalaman kepada luaran, boleh disimulasikan secara berangka. Dengan momen inersia tensor dalaman tetap objek = $\scriptstyle {\boldsymbol {I}}_{0}$ dan momentum sudut luaran tetap = $\scriptstyle {\boldsymbol {L}}$ , maka halaju sudut seketikanya ialah $\scriptstyle {\boldsymbol {\omega }}({\boldsymbol {R}})\;=\;{\boldsymbol {R}}{\boldsymbol {I}}_{0}^{-1}{\boldsymbol {R}}^{T}{\boldsymbol {L}}$ . Liukan berlaku dengan berulang-kali menghitung semula ${\boldsymbol {\omega }}$ serta menggunakan vektor putaran yang kecil $\scriptstyle {\boldsymbol {\omega }}dt$ untuk jangka masa singkat $\scriptstyle dt$ ; cth. $\scriptstyle {\boldsymbol {R}}_{\text{new}}\;=\;\exp([{\boldsymbol {\omega }}({\boldsymbol {R}}_{\text{old}})]_{\times }dt){\boldsymbol {R}}_{\text{old}}$ untuk matriks simetri pencong $\scriptstyle [{\boldsymbol {\omega }}]_{\times }$ . Ralat-ralat yang diaruh oleh langkah-langkah masa yang terhingga cenderung meningkatkan tenaga kinetik putaran, $\scriptstyle E({\boldsymbol {R}})\;=\;{\boldsymbol {\omega }}({\boldsymbol {R}})\cdot {\boldsymbol {L}}/2$ ; kecenderungan tak fizik ini boleh dineutralkan dengan berulang-kali menggunakan vektor putaran kecil $\scriptstyle {\boldsymbol {v}}$ yang serenjang kepada kedua-dua $\scriptstyle {\boldsymbol {\omega }}$ dan $\scriptstyle {\boldsymbol {L}}$ sekali dengan mengambil kira bahawa $\scriptstyle E(\exp([{\boldsymbol {v}}]_{\times }){\boldsymbol {R}})\;\approx \;E({\boldsymbol {R}})\,+\,({\boldsymbol {\omega }}({\boldsymbol {R}})\,\times \,{\boldsymbol {L}})\cdot {\boldsymbol {v}}$ .

Teraruh tork

Liukan teraruh tork (liukan giroskop) adalah fenomena yang mana paksi objek berputar (cth. giroskop) menghuraikan suatu bentuk kon dalam ruang apabila dikenakan tork luaran. Fenomena ini sering kelihatan pada gasing berputar, tetapi semua objek berputar boleh menjalani liukan. Jika kelajuan putaran dan magnitud tork luaran adalah malar, maka paksi putaran akan bergerak pada sudut tegak kepada arah yang berpunca dengan intuitif daripada tork luaran. Dalam hal gasing, beratnya bertindak ke arah bawah daripada pusat jisimnya sementara daya normal (reaksi) landasnya tertolak ke atas hingga ke titik pertemuan dengan sokongan. Kedua-dua daya bertentangan ini menghasilkan tork yang menyebabkan gasing meliuk.

Tindak balas sistem berputar kepada tork yang dikenakan. Apabila gimbal berpusing, bahkan dibubuh dengan golekan, maka rodanya mudah beranggul.

Peranti yang digambarkan di sebelah kanan ialah gimbal bercagak. Dari dalam ke luarnya terdapat tiga paksi putaran, iaitu hab roda, paksi gimbal, dan pangsi menegak.

Untuk membezakan dua paksi mengufuk ini, putaran di keliling hab roda dipanggil pusingan, sementara putaran di keliling paksi gimbal dipanggil anggulan. Putaran di keliling pangsi menegak pula dipanggil putaran.

Mula-mula, bayangkan seluruh peranti berputar di keliling paksi pangsi (menegak). Kemudian ditambahnya pusingan roda (di keliling hab roda). Bayangkan paksi gimbal terkunci supaya roda tidak boleh beranggul. Paksi gimbal mempunyai pengesan yang menyukat kehadiran tork di keliling paksi gimbal.

Dalam gambarajah, sebahagian roda itu dinamakan dm₁. Pada seketika yang digambarkan, bahagian dm₁ berada di perimeter pergerakan berputar di keliling paksi pangsi (menegak). Ole itu bahagian dm₁ mempunyai banyak halaju putaran sudutan berhubungan dengan putaran di keliling paksi pangsi, bahkan memandangkan dm₁ dipaksa lebih dekat kepada paksi putaran pangsi (oleh roda yang berpusing lama lagi), disebabkan kesan Coriolis berhubung dengan paksi pangsi menegak, dm₁ cenderung bergerak kepada arah anak panah kiri atas dalam gambarajah (pada 45°) dalam arah putaran di keliling pangsi.^[3] Bahagian dm₂ pada roda bergerak pergi dari pangsi, maka suatu daya (iaitu daya Coriolis lagi) bertindak pada arah yang sama seperti dalam dm₁. Perhatikan bahawa kedua-dua anak panah menghala ke arah yang sama.

Hujah yang sama berkenaan untuk separuh bawah roda, tetapi anak-anak panahnya menunjuk ke arah yang bertentangan daripada anak-anak panah yang atas. Yang bergabung di seluruh roda adalah tork di keliling paksi gimbal apabila ditambahnya sedikit pusingan pada putaran di kitar paksi menegak.

Harus diambil kira bahawa tork di keliling paksi gimbal timbul tanpa sebarang pertundaan, maka tindak balasnya adalah serta-merta.

Astronomi

Dalam bidang astronomi, liukan bermaksud sebarang perubahan aruhan graviti yang perlahan dan selanjar di dalam paksi putaran atau laluan orbit sesebuah jasad samawi. Liukan ekuinoks, liukan perihelion, perubahan dalam kecondongan paksi Bumi kepada orbitnya, dan keeksentrikan orbit Bumi selama berpuluh ribu tahunnya, kesemua itu adalah perkara-perkara penting dalam teori astronomi zaman ais.

Liukan paksi (liukan ekuinoks)

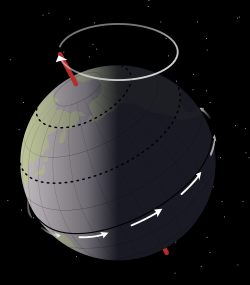
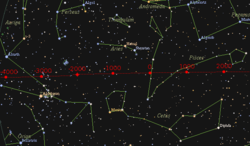
Liukan paksi adalah pergerakan paksi putaran sesebuah jasad samawi yang mana paksinya perlahan-lahan melakarkan sebuah bentuk kon. Dalam hal planet Bumi, liukan sebegini juga dikenali sebagai liukan ekuinoks, liukan qamari-suria, atau liukan khatulistiwa. Bumi melengkapi satu liukan paksi dalam jangka masa kira-kira 26,000 tahun atau 1° setiap 72 tahun, ketika kedudukan bintang-bintang berubah dengan perlahan dalam koordinat khatulistiwa dan garis bujur gerhana. Sepanjang kitaran ini kutub paksi utara Bumi bergerak dari tempatnya sekarang iaitu dalam 1° dari Polaris, di dalam bulatan di sekitar kutub gerhana dengan jejari sudut sekitar 23.5 darjah.

Hipparchus adalah ahli astronomi terkenal terawal yang mengenali dan menilai liukan ekuinoks pada sekitar 1° seabad (yang tidak jauh bezanya dengan nilai sebenar iaitu 1.38°). Liukan paksi Bumi kemudiannya diterangkan oleh fizik Newton. Bumi berbentuk sferoid buntal, iaitu tidak benar-benar sfera tetapi membonjol di khatulistiwa. Daya pasang surut daripada graviti Bulan dan Matahari mengenakan tork ke atas khatulistwa, cuba menarik bonjol khatulistiwa ke dalam satah ekliptik, tetapi sebaliknya menyebabkan ia meliuk. Tork yang didorong oleh planet-planet lain, terutamanya Musytari, turut memainkan peranan.^[4]

Liukan perihelion

Planet yang mengitari matahari mengikut orbit elips (bujur) yang berputar beransur-ansur sepanjang masa (liukan apsis). Keeksentrikan elips ini serta kadar liukan orbit dibesar-besarkan untuk pemvisualan. Kebanyakan orbit dalam Sistem Suria mempunyai keeksentrikan yang lebih rendah dan meliuk pada kadar yang jauh lebih perlahan, oleh itu jadinya hampir-hampir bulat dan pegun.

Orbit sesebuah planet di keliling Matahari bukanlah bujur sepenuhnya, tetapi sebaliknya berbentuk kelopak bunga kerana paksi utama setiap orbit elips planet juga meliuk di dalam satah orbitnya, antara lainnya sebagai balasan kepada usikan dalam bentuk daya-daya graviti berubah-ubah yang didorong oleh planet-planet lain. Ini dipanggil liukan perihelion atau liukan apsis.

Percanggahan antara kadar liukan perihelion tercerap ke atas planet Utarid dengan kadar yang diramal oleh ilmu mekanik klasik adalah terampil dalam kalangan bentuk-bentuk bukti uji kaji yang menjurus kepada penerimaan teori kerelatifan Einstein (khususnya teori kerelatifan am) yang tepat meramal anomalinya. Teori gravitasi Einstein menyimpang dari hukum Newton dengan meramal sebutan tambahan A/r4 yang tepat memberikan kadar belok lebihan tercerap sebanyak 43 arkasaat setiap 100 tahun.

Daya kegravitian antara Matahari dan Bulan mengaruh liukan dalam orbit Bumi, iaitu punca utama ayunan iklim Bumi yang tempohnya 19,000 ke 23,000 tahun. Diturutinya bahawa perubahan parameter orbit Bumi (cth. kecondongan orbit, sudut antara paksi perputaran Bumi dan satah orbitnya) adalah penting untuk mengkaji iklim Bumi, terutamanya untuk mengkaji zaman-zaman ais yang lalu.

Rujukan

^ Schaub, Hanspeter (2003), Analytical Mechanics of Space Systems, AIAA, m/s. 149–150, ISBN 9781600860270, dicapai pada May 2014 Check date values in: |accessdate= (bantuan)
^ Boal, David (2001). "Lecture 26 – Torque-free rotation – body-fixed axes" (PDF). Dicapai pada 2008-09-17.
^ Teodorescu, Petre P (2002). Mechanical Systems, Classical Models. Springer. m/s. 420.
^ Bradt, Hale (2007). Astronomy Methods. Cambridge University Press. m/s. 66. ISBN 978 0 521 53551 9.

[1] Schaub, Hanspeter (2003), Analytical Mechanics of Space Systems, AIAA, m/s. 149–150, ISBN 9781600860270, dicapai pada May 2014 Check date values in: |accessdate= (bantuan)

[2] Boal, David (2001). "Lecture 26 – Torque-free rotation – body-fixed axes" (PDF). Dicapai pada 2008-09-17.

[Teodorescu-3] Teodorescu, Petre P (2002). Mechanical Systems, Classical Models. Springer. m/s. 420.

[Bradt-4] Bradt, Hale (2007). Astronomy Methods. Cambridge University Press. m/s. 66. ISBN 978 0 521 53551 9.

[1]

[2]

[3]

[4]