Kitaran Rankine merupakan sebuah model matematik yang digunakan untuk meramal prestasi enjin stim. Kitaran Rankine merupakan kitaran termodinamik unggul bagi sebuah enjin haba yang menukar haba kepada kerja mekanikal. Haba yang dibekalkan dari luar ke dalam gelung tertutup, yang lazimnya menggunakan air sebagai bendalir kerja. Kitaran Rankine, dalam bentuk enjin stim menjana lebih kurang 90% semua kuasa elektrik yang digunakan di seluruh dunia,[1] termasuk terma suria, biojisim, arang batu dan nuklear. Model ini dinamakan sempena William John Macquorn Rankine, seorang profesor Universiti Glasgow.
Pernyataan

Kitaran Rankine memerihalkan tentang proses enjin haba operasian stim yang lazim ditemui dalam loji penjanaan kuasa terma. Sumber haba yang digunakan bagi loji kuasa tersebut lazimnya dari pembelahan nuklear atau pembakaran bahan api fosil seperti arang batu, gas asli dan minyak.
Kecekapan kitaran Rankine dihadkan oleh haba tinggi pengewapan bendalir kerja. Juga, melainkan tekanan dan suhu mencecah tahap super genting dalam dandang stim, julat suhu bagi kitaran yang boleh beroperasi adalah kecil: suhu masukan turbin stim lazimnya 565°C (had rayapan keluli tahan karat) dan suhu kondenser adalah sekitar 30°C. Ini memberikan kecekapan Carnot maksimum secara teorinya adalah lebih kurang 63% berbanding kecekapan terma keseluruhan sebenar yang mencecah 42% bagi stesen kuasa arang batu yang moden. Suhu masukan wap turbin yang rendah ini (jika dibandingkan dengan turbin gas) adalah penyebab kitaran Rankine (stim) sering digunakan sebagai kitaran pengalas untuk memulihkan haba yang hendak dibuang dalam stesen kuasa turbin gas gabungan kitaran.
Bendalir kerja dalam kitaran Rankine mengikut gelung tertutup dan sering digunakan semula. Wap air dengan titisan terkondensasi sering dilihat menggelora dari stesen kuasa yang dicipta oleh sistem penyejukan (bukan secara terus dari kitaran kuasa Rankine gelung tertutup) dan memberi makna bagi haba buangan (suhu rendah) untuk keluar daripada sistem, lalu membenarkan penambahan haba (suhu tinggi) yang boleg ditukar kepada kerja yang lebih berguna (kuasa). Haba 'ekzos' ini diwakili oleh "Qout" yang mengalir keluar dari sisi bawah kitaran seperti yang ditunjuk dalam rajah T/S. Menara penyejuk beroperas sebagai penukar haba yang besar dengan menyerap haba pengewapan pendam bagi bendalir kerja dan, pada masa yang sama, menyejat air penyejuk ke atmosfera. Sementara banyak bahan digunakan sebagai bendalir kerja dalam kitaran Rankine, air sering digunakan sebagai bendalir pilihan kerana sifatnya yang lebih disenangi, iaitu bahan kimia yang tidak bertoksik dan bertindak balas, mudah diperolehi, kos rendah dan sifat termodinamiknya. Dengan memeluwap stim kerja kepada cecair, tekanan di keluaran turbin adalah direndahkan dan tenaga yang diperlukan untuk pam suapan memakan hanya 1 hingga 3% kuasa keluaran turbin dan faktor inilah yang menyumbang kepada kecekapan yang lebih tinggi bagi satu-satu kitaran. Kelebihan kitaran ini diimbangi dengan stim bersuhu rendah yang dimasukkan ke dalam turbin. Turbin gas, sebagai contoh, mempunyai suhu masukan turbin yang menghampiri 1500°C. Walau bagaimanapun, kecekapan terma bagi stesen kuasa stim yang besar dan stesen turbin gas yang moden adalah sama.
Empat proses dalam Kitaran Rankine
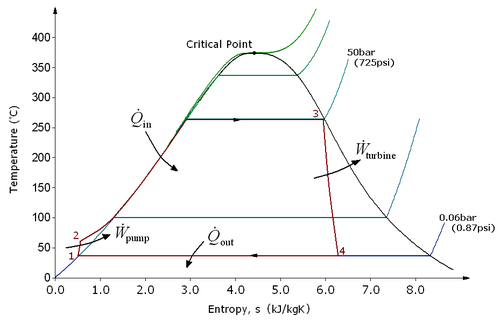
Terdapat empat proses dalam kitaran Rankine. Keadaan ini dikenalpasti dengan nombor (berwarna perang) dalam rajah TS.
- Proses 1-2: Bendalir kerja dipam dari tekanan rendah ke tekanan tinggi. Memandangkan bendalir adalah cecair peringkat ini, pam memerlukan sedikit tenaga masukan tambahan.
- Proses 2-3: Cecair bertekanan tinggi memasuki sebuah dandang lalu akan dipanaskan pada tekanan malar oleh sumber habat luaran untuk menjadi wap tepu yang kering. Tenaga masukan yang diperlukan boleh dikira dengan mula menggunakan rajah mollier atau carta h-s atau carta entalpi-entropi yang turut dikenali sebagai jadual stim.
- Proses 3-4: Wap tepu kering mengembang melalui turbin, menjana kuasa. Hal ini mengurangkan suhu dan tekanan wap, dan pemeluwapan mungkin berlaku. Keluaran dalam proses ini boleh dikira dengan mudah dengan menggunakan carta entalpi-entropi atau jadual stim.
- Proses 4-1: Wap basah kemudiannya memasuki sebuah pemeluwap untuk dijadikan wap pada suhu malar supaya menjadi cecair tepu.
Dalam kitaran Rankine yang unggul,pam dan turbin akan mengalami fasa isentropi, iaitu pam dan turbin akan menjana sifar entropi lalu memaksimumkan kerja keluaran bersih. Proses 1-2 dan 3-4 diwakili oleh garisan menegak pada rajah T-S dan lebih menyerupai kitaran Carnot. Kitaran Rankine yang ditunjukkan di sini mengelakkan dari wap berakhir dalam kawasan superhaba selepas pengembangan dalam turbin, [1] yang mengurangkan tenaga yang dibuang oleh pemeluwap.
Pembolehubah
| Kadar pengaliran haba ke atau dari sistem (tenaga per unit masa) | |
| Kadar pengaliran jisim (jisim per unit masa) | |
| Kuasa mekanikal yang digunakan oleh atau dihasilkan untuk sistem (tenaga per unit masa) | |
| Kecekapan termodinamik bagi proses (kuasa bersih per masukan haba, tiada dimensi) | |
| Kecekapan isentropi bagi proses pemampatan (pam suapan) dan pengembangan (turbin), tiada dimensi | |
| "Entalpi tentu" pada titik yang dinyatakan pada rajah T-S | |
| "Entalpi tentu" akhir bagi bendalir jika turbin adalah isentropi | |
| Tekanan sebelum dan selepas proses pemampatan |
Persamaan
Secara umumnya, kecekapan bagi kitaran Rankine ringkas boleh ditakrifkan sebagai:
Setiap empat persamaan seterusnya[1] boleh diterbitkan secara mudah dari tenaga dan baki jisim bagi isi padu yang terkawal. menakrifkan kecekapan termodinamik bagi kitaran tersebut sebagai nisbah keluaran kuasa bersih dengan masukan haba. Memandangkan kerja yang diperlukan pam lazimnya sekitar 1% daripada keluaran kerja turbin, ia boleh dipermudahkan.
Apabila berhadapan dengan kecekapan turbin dan pam, penyesuaian untuk kerja harus dibuat.
Rujukan
- ^ Wiser, Wendell H. (2000). Energy resources: occurrence, production, conversion, use. Birkhäuser. m/s. 190. ISBN 978-0-387-98744-6.
- ^Van Wyllen 'Fundamentals of thermodynamics' (ISBN 85-212-0327-6)
- ^Wong 'Thermodynamics for Engineers',2nd Ed.,2012, CRC Press, Taylor & Francis, Boca Raton, London, New York. (ISBN 978-1-4398-4559-2)
- Moran & Shapiro 'Fundamentals of Engineering Thermodynamics' (ISBN 0-471-27471-2)
- Wikibooks Engineering Thermodynamics























