Blaise Pascal | |
|---|---|
 Lukisan Blaise Pascal dilukis oleh François II Quesnel untuk Gérard Edelinck pada 1691 | |
| Kelahiran | 19 Jun 1623 |
| Meninggal dunia | 19 Ogos 1662 (umur 39) Paris, Perancis |
| Warganegara | Perancis |
| Era | Falsafah abad ke-17 |
| Falsafah | Falsafah Barat |
| Sekolah | Jansenisme |
Kepentingan utama | |
Idea cemerlang | |
Blaise Pascal (Perancis: [blɛz paskal]); (19 Jun 1623 – 19 Ogos 1662) adalah seorang ahli matematik Perancis, ahli fizik, pencipta, penulis dan ahli teologi Katolik. Dia adalah seorang anak ajaib yang dididik oleh bapanya, pemungut cukai di Rouen. Kerja-kerja terawal Pascal adalah dalam sains semulajadi dan gunaan di mana beliau membuat sumbangan penting dalam kajian cecair, dan menjelaskan konsep tekanan dan vakum dengan mengadaptasi karya Evangelista Torricelli. Pascal juga menulis bagi mempertahankan kaedah saintifik.
Pada tahun 1642, semasa masih remaja, beliau memulakan beberapa kerja perintis untuk mesin mengira. Selepas tiga tahun usaha dan 50 prototaip,[2] beliau membina 20 mesin siap (dipanggil Mesin kira Pascal dan kemudian Pascalines) dalam tempoh 10 tahun berikutnya,[3] menjadikannya sebagai salah satu daripada dua pencipta kalkulator mekanik pertama.
Pascal adalah seorang ahli matematik penting yang telah membantu mencipta dua bidang utama penyelidikan baru: beliau menulis sebuah karya penting mengenai subjek geometri projektif pada usia 16 tahun, dan kemudiannya bersama dengan Pierre de Fermat berkenaan teori kebarangkalian,yang sangat mempengaruhi pembangunan ekonomi moden dan sains sosial. Mengikuti Galileo Galilei dan Evangelista Torricelli, pada tahun 1647, dia membantah pengikut Aristotle yang menegaskan bahawa alam semulajadi terdiri sepenuhnya material dan tiada kaitan dengan vakum. Keputusan Pascal menyebabkan banyak pertikaian sebelum diterima oleh masyarakat.
Pada tahun 1646, dia dan kakaknya, Jacqueline mengenal pasti gerakan agama dalam Katolik yang dikenali oleh pengkritiknya sebagai Jansenisme. Pascal mengikuti pergerakan agama pada akhir 1654 dan beliau mula menulis karya berpengaruh berkenaan falsafah dan teologi. Dua karya yang paling terkenal pada ketika itu: Lettres Provinciales dan Pensées, yang pertama ditulis ketika konflik antara Jansenis dan Jesuit. Pada tahun itu, beliau juga menulis satu karya penting mengenai segitiga aritmetik. Antara tahun 1658 dan 1659, dia telah menulis mengenai sikloid dan penggunaannya dalam menghitung jumlah pepejal.
Sepanjang hidupnya, Pascal berada dalam keadaan kesihatan yang lemah, terutama selepas usia 18 tahun; dia meninggal dunia hanya dua bulan selepas hari jadi ke-39.[4]
Kehidupan awal dan Pendidikan
Pascal dilahirkan di Clermont-Ferrand, yang terletak di rantau Auvergne, Perancis. Dia kehilangan ibunya, Antoinette Begon, pada usia tiga tahun. [5] Ayahnya, Étienne Pascal (1588-1651), yang juga mempunyai minat dalam sains dan matematik, adalah seorang hakim tempatan dan ahli Noblesse de Robe. Pascal mempunyai dua adik perempuan, Jacqueline yang lebih muda dan yang sulung, Gilberte.
Pada tahun 1631, lima tahun selepas kematian isterinya,[6] Étienne Pascal berpindah dengan anak-anaknya ke Paris. Keluarga yang baru tiba tidak lama lagi mengupah Louise Delfault, seorang pembantu rumah yang akhirnya menjadi ahli keluarga mereka. Étienne, yang tidak pernah berkahwin semula, memutuskan bahawa dia sendiri akan mendidik anak-anaknya, kerana mereka semua menunjukkan kemampuan intelektual yang luar biasa, terutama anaknya, Blaise. Pada usia muda, Pascal menunjukkan kebolehan yang luar biasa dalam matematik dan sains.
Perkara yang menarik perhatian Pascal adalah karya Desargues mengenai kepingan kon. Berikutan pemikiran Desargues, Pascal yang berusia 16 tahun telah menghasilkan sebuah penulisan sebagai bukti kepada ideologi tersebut iaitu sebuah karya ringkas mengenainya yang disebut "Mystic Hexagram", Essai pour les coniques ("Karangan berkenaan kon") dan menghantarnya-yang merupakan kerja keras matematik pertamanya ke Père Mersenne di Paris; ia masih terkenal sehingga ke hari ini sebagai teorem Pascal. Ia menyatakan bahawa jika segi enam dilukis dalam bulatan (atau kon) maka akan ada tiga titik persilangan yang bertentangan terletak pada garis (dipanggil garis Pascal).
Sumbangan dalam Matematik
Pascal terus mempengaruhi matematik sepanjang hidupnya.Karyanya Traité du triangle arithmétique ("Karya berkenaan Segitiga Aritmetik") pada 1653 menggambarkan persembahan tabular yang mudah untuk pekali binomial yang kini dipanggil segitiga Pascal. Segitiga juga boleh diwakili:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 2 | 1 | 3 | 6 | 10 | 15 | ||
| 3 | 1 | 4 | 10 | 20 | |||
| 4 | 1 | 5 | 15 | ||||
| 5 | 1 | 6 | |||||
| 6 | 1 |
Dia mentakrifkan nombor dalam segitiga dengan rekursi: Memanggil nombor di dalam baris (m + 1) dan (n + 1) lajur tmn. Kemudian tmn = tm–1,n + tm,n–1, untuk m = 0, 1, 2, ... dan n = 0, 1, 2, ... Dengan syarat sempadan adalah tm,−1 = 0, t−1,n = 0 untuk m = 1, 2, 3, ... dan n = 1, 2, 3, ... Penjana t00 = 1. Pascal menyimpulkan dengan bukti,
Pada tahun 1654, beliau membuktikan identiti Pascal yang mengaitkan jumlah kuasa-kuasa p-bilangan integer positif pertama iaitu p = 0, 1, 2, ..., k.[7]
Pada tahun 1654, dengan bantuan oleh rakannya, Chevalier de Méré, dia berbincang dengan Pierre de Fermat mengenai subjek masalah perjudian, dan dari kolaborasi itu lahirlah teori kebarangkalian matematik.[8] Masalah khusus ialah dua pemain yang ingin menyelesaikan permainan awal dan, memandangkan keadaan semasa permainan, ingin membahagikan taruhan dengan adil, berdasarkan peluang masing-masing memenangi permainan dari titik itu. Dari perbincangan ini, tanggapan mengenai nilai yang diharapkan telah diperkenalkan. Pascal kemudian (dalam Pensées) menggunakan hujah kebarangkalian, Hujah Pascal, membenarkan kepercayaan kepada Tuhan dan kehidupan yang mulia. Kerja yang dilakukan oleh Fermat dan Pascal ke dalam kalkulus kebarangkalian meletakkan asas penting bagi perumusan kalkulus Leibniz.[9]
Sumbangan dalam Fizik
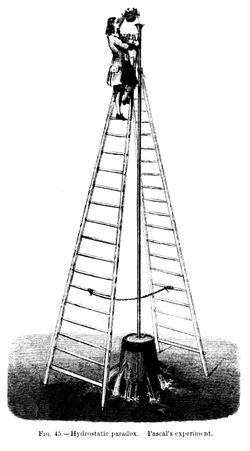
Kerja Pascal dalam bidang kajian hidrodinamik dan hidrostatik yang berpusat pada prinsip cecair hidraulik. Ciptaannya termasuk tekanan hidraulik (menggunakan tekanan hidraulik untuk melipatgandakan daya) dan jarum suntikan. Dia membuktikan bahawa tekanan hidrostatik tidak bergantung kepada berat cecair tetapi pada perbezaan ketinggian. Dia memperlihatkan prinsip ini dengan menyambungkan tiub nipis ke tong yang penuh dengan air dan mengisi tiub dengan air hingga ke tingkat lantai tiga bangunan. Ini menyebabkan tong itu bocor, yang dikenali sebagai eksperimen tong Pascal.
Menjelang 1647, Pascal telah mempelajari eksperimen Evangelista Torricelli dengan menggunakan barometer. Setelah mereplikasi eksperimen yang melibatkan meletakkan tiub yang dipenuhi dengan merkuri terbalik dalam mangkuk merkuri, Pascal mempersoalkan daya apa yang memelihara merkuri di dalam tiub dan apa yang mengisi ruang di atas merkuri dalam tiub. Pada masa itu, kebanyakan saintis berpendapat bahawa, bukannya vakum, terdapat beberapa perkara yang tidak dapat dilihat. Ini berdasarkan kepada idea Aristoteles bahawa penciptaan adalah bahan yang sama, sama ada kelihatan atau tidak kelihatan; dan bahawa bahan ini selamanya bergerak. Tambahan pula, "Segala sesuatu yang bergerak mesti dipindahkan oleh sesuatu," kata Aristoteles.[10] Oleh itu, Aristoteles mempengaruhi saintis-saintis pada masa itu dengan mengatakan bahawa vakum adalah mustahil. Bagaimana dia berbuat demikian? Sebagai bukti, dia menunjukkan:
- Cahaya merentas sesuatu ialah apa yang dipanggil "vakum" dalam tiub kaca.
- Aristotle menulis bagaimana semua benda bergerak, dan mesti dipindahkan oleh sesuatu.
- Oleh itu, kerana perlu ada "sesuatu" yang tidak kelihatan untuk menggerakkan cahaya melalui tiub kaca, tidak ada vakum di dalam tiub. Tidak di dalam tiub kaca atau di mana sahaja. Vakum - ketiadaan apa-apa dan segala-galanya - hanyalah satu kemustahilan.
Berikutan banyak eksperimen yang dilakukan pada salur darah, pada 1647, Pascal telah menghasilkan Experiences nouvelles touchant le vide ("eksperimen baru dengan vakum"), yang menerangkan peraturan asas dengan gambaran tahap darjah pelbagai cecair dipengaruhi oleh tekanan udara. Ia juga menyatakan bahawa tiang cecair dalam tiub barometer ialah vakum berserta sebab-sebabnya. Kerja ini kemudiannya dibukukan, Récit de la grande expérience de l'équilibre des liqueurs ("Akaun percubaan besar terhadap keseimbangan dalam cecair") yang diterbitkan pada tahun 1648.
Kehidupan dewasa, Agama, Falsafah, dan Kesusasteraan
Penukaran agama
Pada musim sejuk tahun 1646, ayah Pascal berusia 58 tahun memecahkan pinggulnya apabila dia tergelincir dan jatuh ke jalan yang berair di Rouen; Mengingat umur lelaki dan keadaan perubatan pada abad ke-17, pinggul yang patah boleh menjadi keadaan yang sangat serius, mungkin juga membawa maut. Rouen adalah rumah kepada dua doktor terbaik di Perancis; Doktor Monsieur Deslandes dan Doktor de La Bouteillerie. Pascal "tidak akan membiarkan orang lain selain daripada orang-orang ini (Doktor Monsieur Deslandes dan Doktor de La Bouteillerie) menguruskan ayahnya... Ini adalah pilihan yang terbaik, supaya orang tua itu (ayah Pascal( selamat dan dapat berjalan lagi ..."[11] Tetapi rawatan dan pemulihan mengambil masa tiga bulan, pada masa itu La Bouteillerie dan Deslandes telah menjadi pelawat biasa.
Kedua-dua lelaki itu adalah pengikut Jean Guillebert, penyokong kumpulan sempit dari ajaran Katolik yang dikenali sebagai Jansenisme. Perkara yang dianggap kecil ini membuat kejutan yang telah mengejutkan masyarakat Katolik Perancis ketika itu. Ia menyokong Augustinisme yang ketat. Blaise bercakap dengan para doktor dengan kerap selepas rawatan mereka yang berjaya terhadap bapanya,dia meminjam karya-karya yang ditulis oleh penulis Jansenis daripada doktor-doktor tersebut. Dalam tempoh ini, Pascal mengalami "penukaran pertama" dan mula menulis mengenai subjek teologi pada tahun berikutnya.
Legasi
Untuk menghargai sumbangan saintifiknya, nama Pascal telah diberikan dalam penggunaan unit SI tekanan, bahasa pengaturcaraan, dan prinsip Pascal (prinsip berkenaan hidrostatik), dan seperti yang disebutkan di atas, segitiga Pascal dan hujah Pasccal masih menggunakan namanya.
Teori kebarangkalian yang diperkenalkan Pascal adalah sumbangannya yang paling berpengaruh kepada matematik. Asalnya digunakan untuk perjudian, hari ini sangat penting dalam ekonomi, terutama dalam sains aktuari. John Ross menulis, "Teori kebarangkalian dan penemuan-penemuan berikut mengubah cara kita menganggap ketidakpastian, risiko, membuat keputusan, dan keupayaan individu dan masyarakat untuk mempengaruhi perjalanan peristiwa masa depan."[12] Walau bagaimanapun, perlu diperhatikan bahawa Pascal dan Fermat, walaupun melakukan kerja awal yang penting dalam teori kebarangkalian, tidak mengembangkan teori ini dengan begitu meluas. Christiaan Huygens, mempelajari subjek dari karya-karya Pascal dan Fermat, lalu menulis buku pertama mengenai subjek itu. Figura yang mengikut perkembangan teori itu termasuk Abraham de Moivre dan Pierre-Simon Laplace.
Rujukan
- ^ Vincent Jullien (ed.), Seventeenth-Century Indivisibles Revisited, Birkhäuser, 2015, p. 188.
- ^ (fr) La Machine d’arithmétique, Blaise Pascal, Wikisource
- ^ Mourlevat, Guy (1988). Les machines arithmétiques de Blaise Pascal (dalam bahasa Perancis). Clermont-Ferrand: La Française d'Edition et d'Imprimerie. m/s. 12.
- ^ Hald, Anders A History of Probability and Statistics and Its Applications before 1750, (Wiley Publications, 1990) pp.44
- ^ Devlin, m/s. 20.
- ^ O'Connor, J.J.; Robertson, E.F. (August 2006). "Étienne Pascal". University of St. Andrews, Scotland. Dicapai pada 5 February 2010.
- ^ Kieren MacMillan, Jonathan Sondow (2011). "Proofs of power sum and binomial coefficient congruences via Pascal's identity". American Mathematical Monthly. 118: 549–551. arXiv:1011.0076. doi:10.4169/amer.math.monthly.118.06.549.
- ^ Devlin, m/s. 24.
- ^ "The Mathematical Leibniz". Math.rutgers.edu. Dicapai pada 16 August 2009.
- ^ Aristotle, Physics, VII, 1.
- ^ Connor, James A., Pascal's wager: the man who played dice with God (HarperCollins, NY, 2006) ISBN 0-06-076691-3 p. 70
- ^ Ross, John F. (2004). "Pascal's legacy". EMBO Reports. 5 (Suppl 1): S7–S10. doi:10.1038/sj.embor.7400229. PMC 1299210. PMID 15459727.
| Umum | |
|---|---|
| Perpustakaan negara | |
| Kamus biografi | |
| Pangkalan data saintifik | |
| Lain-lain |
|
