Daripada Wikipedia, ensiklopedia bebas.
Gelombang ialah satu gangguan yang membawa tenaga melalui medium.
"Gelombang melintang" ialah gelombang yang menyebabkan zarah-zarah medium bergetar berserenjang dengan arah gerakan gelombang.
"Gelombang membujur" pula menyebabkan getaran zarah-zarah medium selari dengan arah gerakan gelombang
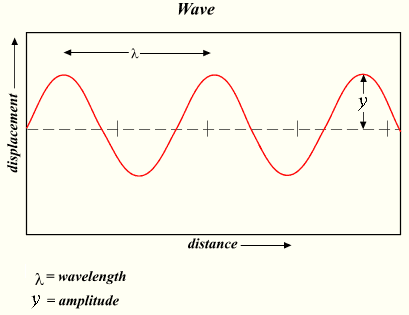
frames Amplitud ,
A
{\displaystyle A\,}
Tempoh ,
T
{\displaystyle T\,}
Panjang gelombang ,
λ
{\displaystyle \lambda \,}
Laju gelombang pula ialah hasil darab frekuensi dan panjang gelombang .
v
=
λ
f
{\displaystyle v=\lambda f\,}
Nombor gelombang ,
k
{\displaystyle k\,}
k
=
2
π
λ
{\displaystyle k={\frac {2\pi }{\lambda }}\,}
Frekuensi ,
f
{\displaystyle f\,}
hertz ) ialah tempoh per unit masa:
f
=
1
T
{\displaystyle f={\frac {1}{T}}\,}
dan frekuensi sudutnya ialah:
ω
=
2
π
f
=
v
k
{\displaystyle \omega =2\pi f=vk\,}
Persamaan gelombang bentuk sinus bergerak ke arah positif x dalam paksi xy ialah:
y
(
x
,
t
)
=
A
c
o
s
[
ω
(
x
v
−
t
)
]
=
A
c
o
s
[
2
π
f
(
x
v
−
t
)
]
{\displaystyle y(x,t)=Acos[\omega ({\frac {x}{v}}-t)]=Acos[2\pi f({\frac {x}{v}}-t)]}
=
A
c
o
s
[
2
π
(
x
λ
−
t
T
)
]
=
A
c
o
s
(
k
x
−
ω
t
)
{\displaystyle =Acos[2\pi ({\frac {x}{\lambda }}-{\frac {t}{T}})]=Acos(kx-\omega t)\,}
Manakala bagi gerakan gelombang ke arah negatif x ialah:
y
(
x
,
t
)
=
A
c
o
s
[
ω
(
x
v
+
t
)
]
=
A
c
o
s
[
2
π
f
(
x
v
+
t
)
]
{\displaystyle y(x,t)=Acos[\omega ({\frac {x}{v}}+t)]=Acos[2\pi f({\frac {x}{v}}+t)]}
=
A
c
o
s
[
2
π
(
x
λ
+
t
T
)
]
=
A
c
o
s
(
k
x
+
ω
t
)
{\displaystyle =Acos[2\pi ({\frac {x}{\lambda }}+{\frac {t}{T}})]=Acos(kx+\omega t)\,}
Halaju zarah-zarah (Bukan Laju Gelombang )dalam gelombang bentuk sinus ialah:
v
y
→
=
δ
y
(
x
,
t
)
δ
t
=
ω
A
s
i
n
(
k
x
−
ω
t
)
{\displaystyle {\vec {v_{y}}}={\frac {\delta y(x,t)}{\delta t}}=\omega Asin(kx-\omega t)\,}
manakala pecutannya ialah:
a
y
→
=
δ
(
x
,
t
)
δ
t
=
−
ω
2
A
c
o
s
(
k
x
−
ω
t
)
=
−
ω
2
y
(
x
,
t
)
{\displaystyle {\vec {a_{y}}}={\frac {\delta (x,t)}{\delta t}}=-\omega ^{2}Acos(kx-\omega t)=-\omega ^{2}y(x,t)\,}
Persamaan gelombang ialah persamaan pembezaan yang menyentuh sifat-sifat fizikal gelombang yang melalui suatu medium. Kerana tidak semua gelombang berbentuk sinus, maka persamaan am gelombang ialah:
δ
2
y
(
x
,
t
)
δ
x
2
=
1
v
2
δ
2
y
(
x
,
t
)
δ
t
2
{\displaystyle {\frac {\delta ^{2}y(x,t)}{\delta x^{2}}}={\frac {1}{v^{2}}}{\frac {\delta ^{2}y(x,t)}{\delta t^{2}}}\,}


















![{\displaystyle y(x,t)=Acos[\omega ({\frac {x}{v}}-t)]=Acos[2\pi f({\frac {x}{v}}-t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77a7d0ad3747aa06f4b0e3dd012dfc551ac83840)
![{\displaystyle =Acos[2\pi ({\frac {x}{\lambda }}-{\frac {t}{T}})]=Acos(kx-\omega t)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d544419b56638f3473fbc2decca27051d5c605e5)
![{\displaystyle y(x,t)=Acos[\omega ({\frac {x}{v}}+t)]=Acos[2\pi f({\frac {x}{v}}+t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/063bc0508ebd13600a589ae56726082542747f0f)
![{\displaystyle =Acos[2\pi ({\frac {x}{\lambda }}+{\frac {t}{T}})]=Acos(kx+\omega t)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f088a71002a9890c4f2b6620271aaa2ce92463c8)


