Siri Balmer - Wikipedia Bahasa Melayu, ensiklopedia bebas

Garis spektrum pancaran hidrogen "tampak" dalam siri Balmer. H-alfa ialah garis merah di sebelah kanan. Empat garis (dikira dari kanan) secara rasmi dalam julat boleh lihat. Garis lima dan enam boleh dilihat dengan mata kasar, tetapi dianggap sebagai ultraungu kerana ia mempunyai panjang gelombang kurang daripada 400 nm.

Siri Balmer (Jawi: ‏سيري بلمر‎‎), atau garis Balmer dalam fizik atom, adalah satu daripada set enam siri bernama yang menerangkan garis spektrum pancaran bagi atom hidrogen. Siri Balmer dikira menggunakan rumus Balmer, persamaan empirik yang ditemui oleh Johann Balmer pada tahun 1885.

Spektrum cahaya yang boleh dilihat daripada hidrogen memaparkan empat panjang gelombang, 410 nm, 434 nm, 486 nm, dan 656 nm, yang sepadan dengan pelepasan foton oleh elektron dalam keadaan teruja yang beralih kepada tahap kuantum yang diterangkan oleh nombor kuantum utama n sama dengan 2.^[1] Terdapat beberapa garisan Balmer ultraungu yang menonjol dengan panjang gelombang lebih pendek daripada 400 nm. Siri ini diteruskan dengan jumlah garisan yang tidak terhingga dengan panjang gelombang yang mendekati had 364.5 nm dalam ultraungu.

Selepas penemuan Balmer, lima siri spektrum hidrogen lain juga ditemui, sepadan dengan elektron yang beralih kepada nilai n selain daripada dua.

Gambaran keseluruhan

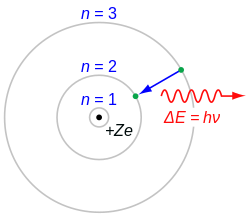
Siri Balmer dicirikan oleh peralihan elektron daripada n ≥ 3 hingga n = 2, di mana n merujuk kepada nombor kuantum jejari atau nombor kuantum utama elektron. Peralihan dinamakan secara berurutan oleh huruf Yunani: n = 3 hingga n = 2 dipanggil H-α, 4 hingga 2 ialah H-β, 5 hingga 2 ialah H-γ, dan 6 hingga 2 ialah H-δ. Memandangkan garis spektrum pertama yang dikaitkan dengan siri ini terletak di bahagian spektrum elektromagnet yang boleh dilihat, garisan ini secara sejarah dirujuk sebagai "H-alfa", "H-beta", "H-gama", dan seterusnya, dengan H ialah unsur hidrogen.

Peralihan n	3→2	4→2	5→2	6→2	7→2	8→2	9→2	∞→2
Nama	H-α / Ba-α	H-β / Ba-β	H-γ / Ba-γ	H-δ / Ba-δ	H-ε / Ba-ε	H-ζ / Ba-ζ	H-η / Ba-η	Lonjakan Balmer
Panjang gelombang (nm, udara)	656.279^[2]	486.135^[2]	434.0472^[2]	410.1734^[2]	397.0075^[2]	388.9064^[2]	383.5397^[2]	364.5
Perbezaan tenaga (eV)	1.89	2.55	2.86	3.03	3.13	3.19	3.23	3.40
Warna	Merah	Sian	Biru	Lembayung	(Ultraungu)	(Ultraungu)	(Ultraungu)	(Ultraungu)

Walaupun ahli fizik menyedari pancaran atom sebelum 1885, mereka tidak mempunyai alat untuk meramalkan dengan tepat di mana garis spektrum akan muncul. Persamaan Balmer meramalkan empat garisan spektrum hidrogen yang boleh dilihat dengan ketepatan yang tinggi. Persamaan Balmer mengilhamkan persamaan Rydberg sebagai generalisasi, dan ini seterusnya membawa ahli fizik untuk mencari siri Lyman, Paschen, dan Brackett, yang meramalkan garis spektrum hidrogen lain yang terdapat di luar spektrum boleh dilihat.

Garis spektrum merah H-alfa dalam siri Balmer bagi hidrogen atom, yang merupakan peralihan daripada petala n = 3 kepada petala n = 2, adalah salah satu warna yang ketara di alam semesta. menyumbang kepada garisan merah terang dalam spektrum nebula pancaran atau nebula pengionan, seperti Orion Nebula, yang selalunya kawasan H II yang terdapat di kawasan pembentukan bintang. Dalam gambar warna sebenar, nebula ini mempunyai warna merah jambu-kemerahan yang terhasil daripada gabungan garisan Balmer yang kelihatan yang dipancarkan oleh hidrogen.

Kemudian, didapati bahawa apabila garisan siri Balmer bagi spektrum hidrogen diperiksa pada resolusi yang sangat tinggi, ia adalah dua garisan yang sangat rapat. Pembelahan ini dipanggil struktur halus. Ia juga didapati bahawa elektron yang teruja daripada petala dengan n lebih daripada 6 boleh melompat ke n = 2, memancarkan warna ultraungu apabila berbuat demikian.

Rumus Balmer

Balmer menyedari bahawa satu panjang gelombang mempunyai kaitan dengan setiap garisan dalam spektrum hidrogen yang berada di kawasan cahaya yang boleh dilihat. Panjang gelombang itu adalah 364.50682 nm. Apabila mana-mana integer yang lebih tinggi daripada 2 telah kuasa dua dan kemudian dibahagikan dengan kuasa dua nombor itu dan ditolak dengan 4, nombor itu kemudian didarabkan dengan 364.50682 nm (lihat persamaan di bawah) memberikan panjang gelombang garis lain dalam spektrum hidrogen. Dengan rumus ini, beliau dapat menunjukkan bahawa beberapa ukuran garisan yang dibuat pada zamannya melalui spektroskopiadalah sedikit tidak tepat, dan rumus beliau juga meramalkan garisan yang belum ditemui tetapi kemudiannya dijumpai. Nombor beliau juga membuktikan bahawa ia adalah had bagi siri tersebut. Persamaan Balmer boleh digunakan untuk mencari panjang gelombang garis serapan/pancaran dan pada asalnya dibentangkan seperti berikut (kecuali perubahan notasi untuk memberikan pemalar Balmer sebagai B ): $\lambda \ =B\left({\frac {m^{2}}{m^{2}-n^{2}}}\right)=B\left({\frac {m^{2}}{m^{2}-2^{2}}}\right)$ di mana

λ ialah panjang gelombang.
B ialah pemalar dengan nilai 7000364506820000000♠3.6450682 atau 7002364506820000000♠364.50682 .
m ialah keadaan awal $(m\in \mathbb {N} ,m\geq 1).$
n ialah keadaan akhir $(n\in \mathbb {N} ,n\geq m).$

Pada tahun 1888 ahli fizik Johannes Rydberg mengitlakkan persamaan Balmer untuk semua peralihan hidrogen. Persamaan yang biasa digunakan untuk mengira siri Balmer ialah contoh khusus formula Rydberg dan berikut sebagai penyusunan semula matematik timbal balik yang mudah bagi rumus di atas (secara konvensional menggunakan tatatanda m untuk n sebagai satu-satunya pemalar kamiran yang diperlukan):

${\frac {1}{\lambda }}={\frac {4}{B}}\left({\frac {1}{2^{2}}}-{\frac {1}{n^{2}}}\right)=R_{\mathrm {H} }\left({\frac {1}{2^{2}}}-{\frac {1}{n^{2}}}\right)\quad \mathrm {for~} n=3,4,5,\dots$

di mana λ ialah panjang gelombang cahaya yang diserap/dipancarkan dan R _H ialah pemalar Rydberg untuk hidrogen. Pemalar Rydberg dilihat sama dengan rumus Balmer, dan nilai ini, untuk nukleus berat tak terhingga, ialah 4/6993364506820000000♠3.6450682×10⁻⁷ m = 7007109737315700000♠10973731.57 . ^[3]

Peranan dalam ilmu falak

Siri Balmer amat berguna dalam ilmu falak kerana garisan Balmer muncul dalam banyak objek bintang akibat kelimpahan hidrogen di alam semesta, oleh itu ia sering dilihat dan relatif kuat berbanding garisan daripada unsur lain. Dua garis Balmer pertama sepadan dengan garis Fraunhofer C dan F.

Pengelasan spektrum bintang, yang terutamanya penentuan suhu permukaan, adalah berdasarkan kekuatan relatif garis spektrum, dan siri Balmer khususnya sangat penting. Ciri-ciri lain bintang yang boleh ditentukan dengan analisis dekat spektrumnya termasuk graviti permukaan (yang berkaitan dengan saiz fizikal) dan komposisi.

Memandangkan garisan Balmer sering dilihat dalam spektrum pelbagai objek, ia sering digunakan untuk menentukan halaju jejarian akibat peralihan doppler garisan Balmer. Ini mempunyai kegunaan penting dalam seluruh astronomi, daripada mengesan bintang binari, eksoplanet, objek padat seperti bintang neutron dan lohong hitam (melalui pergerakan hidrogen dalam cakera tokokan di sekelilingnya), mengenal pasti kumpulan objek dengan pergerakan dan asal-usul yang serupa (kumpulan segerak, kelompok bintang, gugusan galaksi, dan serpihan daripada perlanggaran), menentukan jarak (sebenarnya anjakan merah) galaksi atau kuasar, dan mengenal pasti objek yang tidak dikenali melalui analisis spektrumnya.

Garisan balmer boleh muncul sebagai garisan serapan atau pancaran dalam spektrum, bergantung pada sifat objek yang diperhatikan. Dalam bintang, garisan Balmer biasanya dilihat dalam bentuk serapan, dan ia adalah "paling kuat" dalam bintang dengan suhu permukaan kira-kira 10,000 K (jenis spektrum A). Dalam spektrum kebanyakan galaksi berpilin dan tidak teratur, nukleus galaksi aktif, rantau H II dan nebula planetari, garisan Balmer ialah jenis garis pancaran.

Dalam spektrum bintang, garisan H-epsilon (peralihan 7→2, 397.007 nm) sering bercampur dengan garis penyerapan lain yang disebabkan oleh kalsium terion yang dikenali sebagai "H" (nama asal yang diberikan oleh Joseph von Fraunhofer). H-epsilon dipisahkan oleh 0.16 nm daripada Ca II H pada 396.847 nm, dan tidak boleh dileraikan dalam spektrum resolusi rendah. Garis H-zeta (peralihan 8→2) juga bercampur dengan garis helium neutral yang biasa dilihat pada bintang panas.

Lihat juga

Rujukan

^ Nave, C. R. (2006). "Hydrogen Spectrum". HyperPhysics. Georgia State University. Dicapai pada 2008-03-01.
^ ^a ^b ^c ^d ^e ^f ^g Kramida, A., Ralchenko, Yu., Reader, J., and NIST ASD Team (2019). NIST Atomic Spectra Database (ver. 5.7.1), [Online]. Available: https://physics.nist.gov/asd [2020, April 11]. National Institute of Standards and Technology, Gaithersburg, MD. DOI: https://doi.org/10.18434/T4W30F
^ "CODATA Recommended Values of the Fundamental Physical Constants: 2006" (PDF). Committee on Data for Science and Technology (CODATA). NIST.

[1] Nave, C. R. (2006). "Hydrogen Spectrum". HyperPhysics. Georgia State University. Dicapai pada 2008-03-01.

[:0-2] ^ ^a ^b ^c ^d ^e ^f ^g Kramida, A., Ralchenko, Yu., Reader, J., and NIST ASD Team (2019). NIST Atomic Spectra Database (ver. 5.7.1), [Online]. Available: https://physics.nist.gov/asd [2020, April 11]. National Institute of Standards and Technology, Gaithersburg, MD. DOI: https://doi.org/10.18434/T4W30F

[CODATA-3] "CODATA Recommended Values of the Fundamental Physical Constants: 2006" (PDF). Committee on Data for Science and Technology (CODATA). NIST.

[1]

[2]

[3]